The chromatic scale

Is there any divine, or universal reason why the chromatic scale of a keyboard is precisely 12 notes, and not 11 or 13?

… And why are they organized in that specific way… With 7 whites and 5 blacks?

It has something to do with the physical laws, something to do with our ears and the way we perceive sounds, and a little to do with practicality.

Disclaimer: This is a very interesting subject, if you’re into music, sound, recordings, and such. Be aware though, that the article is a bit technical

The magical world of pitches and harmonies.

In the physical world there are sounds. Every sound has a pitch, a frequency, and the frequency is measured in Hertz, Hz. 

An interval between two notes means that the frequency of the two notes is different. The more mathematically logical the relationship is between the notes, the more consonant the interval sounds to our ears. Consonant roughly means that it seems harmonical, pleasant, and in tune. Dissonance means disharmonic, unpleasant, and harsh.

For the vast majority of people, the actual pitch doesn’t really matter. We can’t immediately detect if the song is played in E or E♯. What we hear are the intervals, the distances between the notes, and from them, we decide if the song is pleasant and if the singer and the instruments are in tune or not. That is why we can transpose songs, and play any music in any key, and it sounds just as good.

The mathematical connections between notes

If you double the frequency, you get a pitch exactly one octave up. The A (A4) above the middle C on a keyboard is normally tuned at 440 Hz. The A (A5) one octave up is 880 Hz. And the A (A6) another octave up is 1760 Hz, and so on. 

So, the most simple, mathematically logical relationship is doubling. Consequently, the octave is the most consonant interval. It’s so pleasant and harmonic that we actually use the same name for the notes, all over the keyboard. In this case A. To our ear, they seem like two versions of the same note. 

Consonant intervals

• The most consonant interval is the octave, obtained by doubling. 
• The second most consonant interval is a perfect fifth, which is 3/2 of the original frequency. C to G on a keyboard. 
• The third most consonant is the perfect fourth, 4/3 of the original frequency, C to F on a keyboard. 
• The fourth most consonant interval is the major third 5/4 of the original frequency, and the major sixth 5/3 of the original frequency followed by the minor third and the minor sixth. But now we are closing in on the dissonances. 

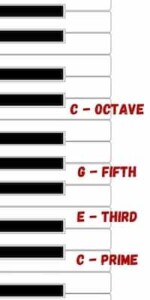
In fact, a harmony, major or minor, consists of three notes, The keynote (the perfect prime), the third (minor or major), and the perfect fifth. And if you look at it, the distance from the fifth to the octave is a perfect fourth. So, there you have the consonant intervals, the prime/octave, the third, the fifth, and the fourth.

Dissonant intervals

• The most dissonant interval is the note halfway between the octave, the diminished fifth, the tritone. It is 17/12 of the original frequency, and as you see, now we’re quite far away from any close connection. 
• The second most dissonant intervals are the minor second 17/16 of the original frequency and the major seventh 19/10 of the original frequency. 
• Other dissonant intervals are the major second, and the minor seventh.
• As the notes in the musical universe aren’t limited to the whites and blacks of a keyboard, even more, dissonant intervals can be obtained by using notes that are in between the semitones of the keyboard. A quarter of a tone, an eighth of tone. But more about that later.

The diatonic scale

The diatonic scale, which is the basis for all western, traditional music theory, is made of 5 whole tones and 2 semitones. The whites of the keyboard.

• On a major scale the sequence of the intervals is 1 – 1 – ½ – 1 – 1 – 1 – ½. 
• If you do these intervals, it doesn’t matter where you start on the keyboard. The intervals will produce a perfect major diatonic scale. 
• The C major scale is C – D – E – F – G – A – B – (C)

Overtones

Any note played by any instrument or sung by a voice, has overtones. The only sound that doesn’t have overtones is a computer-generated sinus tone, sine wave. 

The overtones come from the simultaneous vibration of different parts of the vibrating object. Let’s take the cord of a guitar. When the cord vibrates in its full length, it also vibrates in its half length, and the third of its length and so on. So even if the full length of the cord produces the note that we want, the half cord produces a very weak octave, the third of the cord a very weak fifth over the octave, and so on. These overtones, their distribution and strength, give the sound its character. And together with the attack of the note, they let us distinguish a guitar from a flute, a piano from a voice, etc.

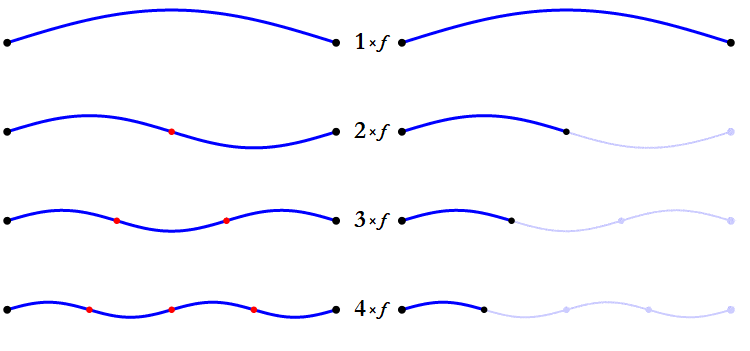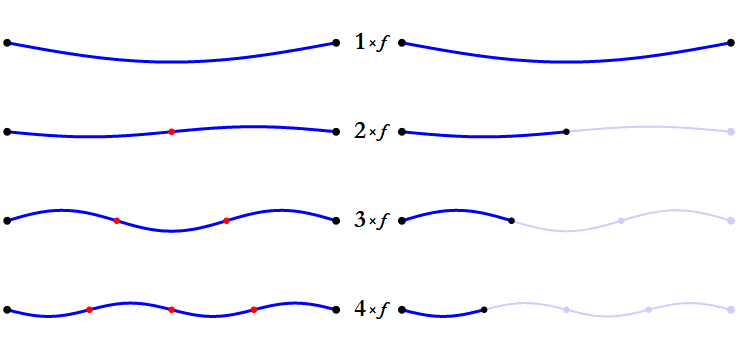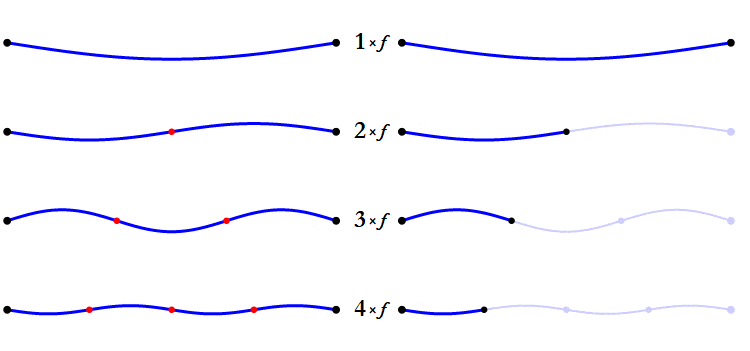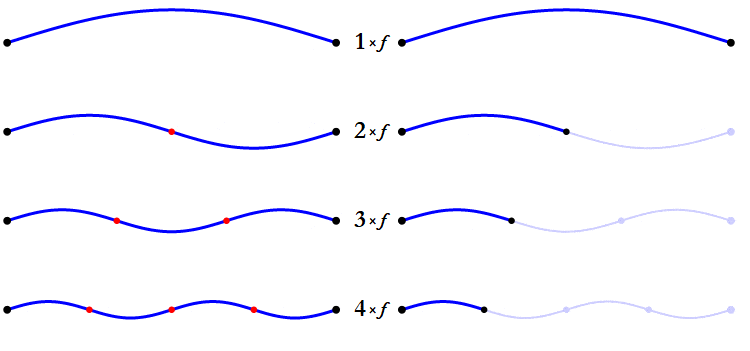
As you can see, the overtones match the consonant intervals pretty accurately.

Now, let’s say we have five of the overtones in a C-note. That would be C – C – G – C – E. 

The special case of the dominant.

The fifth note in music theory is called the dominant, and a chord made up from the fifth note of the scale is the dominant harmony. It has a very close and special relationship to the first note. It would be the G in the C-scale, and any harmony built up from the fifth note of any scale is privileged, and special. 

If we do the same overtone-trick from the G note but with seven notes, we’ll get G – G – D – G – B – D – F.  

If you combine the two overtone series, you get C – D – E – F – G –  – B. It’s not a perfect C scale, but it’s close. The only note missing is A.

Another way to get to a diatonic major scale is playing perfect fifths in a sequencE. You will have to start from a fifth below the C… F – C – G – D – A – E – B.

And you can play a series of thirds, minor and major… A – C – E – G – B – D – F (A technique that is used very frequently in jazz…)

Or it can be described as two tetrachords.

… But these are more of an intellectual – philosophical description, that doesn’t really add anything to the understanding of why the chromatic scale has 12 notes and the diatonic scale has 7.  

The thing to remember here, is that there is a physical relationship between the notes in a consonant harmony, and thus in a consonant diatonic scale. The notes are not just there by chance.

The chromatic scale

So, the diatonic scale is made of 5 whole tones and 2 semitones, the whites of the keyboard. 

If, instead of using whole tones and semitones, we just use the semitones. Then you would have to fill up the 5 whole steps with the half step that lies between. Since there are 5 whole steps in a diatonic scale, you have to add five semitones to get a scale of only half steps, a chromatic scale. 7 + 5 makes 12.

The chromatic scale is the 12 semitones equally distributed between one note and the same note one octave up or down. This perfectly equal distribution is called temperament, and it’s a compromise between the perfect pitch of the natural tones, and the practical need to be able to play in any key.

But it doesn’t necessarily have to be 7… There are many other ways to combine the notes.

During the centuries, and in different parts of the world, various ideas of tuning and constructing scales have been offered. 

• Maybe most notable is the pentatonic scale: With the major third C – D – E – G – A. 
• Or with the minor third A – C – D – E – G
• The hexatonic whole tone scale C – D – E – F# – G# – A# 
• The hexatonic blues scale C – E♭/E (gliding pitch) – F – F# – G – B♭

And there have been many others. All these different ways to combine notes normally still consider the fifth and the fourth as fundamental. Their close connection to the unison, the keynote, make them indispensable in most scales.

And it doesn’t necessarily have to be 12 notes in the chromatic scale either… 

There are numerous other ways to separate the different notes from each other. Here are just a few examples, but there are so many more used in different time periods, and in different regions. 

• You could for example double the number and tune the scale in 24 steps.

• Or you could use 19 steps, which in some way would be rather close to the 12 tone scale, with a few notes added. 
• The 72 equal temperament, or 72 edo divides the octave into 72 equal steps.
• The Byzantine music theory uses the 72 equal temperament scale 
• The Arab tone system is based on 24 equal steps in the octave.

The problems with alternative scales.

The difficulties become obvious when you actually try to play music. How do you play a note that is between one and the other? A keyboard would have to be completely reconstructed. But even instruments like a violin are still constructed to play the 12 notes of the chromatic scale.

And the preparation, and training of the musician often doesn’t prepare him for playing between the notes.

The only real exception would be the voice. A human voice doesn’t have finger positions where the note should be. A singer tunes with the ears and sings according to what he/she hears. The Arabic singer who is trained in a 24 note scale can produce a perfect intonation within that scale. 

The wonderful compromise of the 12-tone equal temperament.

If you have a keyboard tuned in just intonation, and you start from C and put E, and G on top of it, you end up with a beautiful C major chord. Now, if you start from G and put B, and D on it you will have a G major. But while the interval between C and G is a perfect 5th, the interval between G and D is not. Remember that the keyboard was tuned perfectly with the C as the root. The G is in perfect tune compared to the C, but not compared to the D. 

And the further away you get from C, the more out of tune the instrument would seem. G♭ major would sound quite awful. 

If you look at old classical music, before the 18th century, they almost never used keys with a lot of flats or sharps. It didn’t sound well at the time. 

To resolve this, we use something called a temperate tuning system. Instead of tuning the various intervals perfectly, we tune only the octave perfectly, by doubling the frequency. Then we distance the 12 semitones in between equally. Every half note has the exact same space, 100 cents. 

The distance of an octave is 1200 cents.

At the end, the piano is slightly out of tune, but it’s so little that you don’t hear it. The benefit is that you can play in any key and it sounds just as good as in any other.  

So, it’s easy to hear that the last chord is out of tune. If the keyboard is tuned in just intonation with the C note as a base, the C# will come out quite distorted, as it has 5 sharps. 

J.S. Bach and the Well-Tempered Clavier.

In the beginning of 1700 Johann Sebastian Bach wrote two books of 24 preludes and fugues in each. They were equally distributed between the 12 keys. He wrote them in enthusiasm over the newly invented temperature. Something that permitted composting in any key with equally good results.

In the 16th and 17th centuries there had been many suggestions to resolve the problem with the equal temperature, and not even Bach had our modern equal temperature at his disposal. It would take more than a hundred years before the equal 12 tone temperament was widely accepted. The two books with the total of 24 preludes and 24 fugues are regarded today as masterpieces of technical perfection. 

Conclusion

The scales and music theories of the world depend very strongly on traditions, preferences, practicality, and fashions and trends. Still, the foundation for the 7-tone diatonic scale, the 12-tone chromatic scale, as well as almost all other scales, to at least some degree is the physical relations between the various natural overtones of any pitch… The vibration of the half cord, the third of a cord, the fourth, and so on.

Back to the top of the page

home

sources

• Britannica / Overtones
• University of Connecticut, Department of physics / Overtone Series, Addition of Waves and Tone Quality
• American Journal of Physics / The physics of musical scales: Theory and experiment
• Fisica onde Musica / Come si costruiscono le scale pitagoriche?
• Wikipedia / Chromatic scale 
• Wikipedia / Diatonic scale
• Wikipedia / Musica and Mathematics